Tous ces exemples sont intéressants, mais les billes sont rarement aussi bien disposées dans l’un ou l’autre des carrés contingents du billard.

L’idée m’est ainsi venue du ‘carré imaginaire’, c’est-à-dire de déplacer mentalement le carré en fonction de la position de B2 qui prendrait ainsi une position horizontale ‘0’.

Ceci permet de simplifier les calculs et la prévision des trajectoires.                       

5-1  LE CARRE IMAGINAIRE.

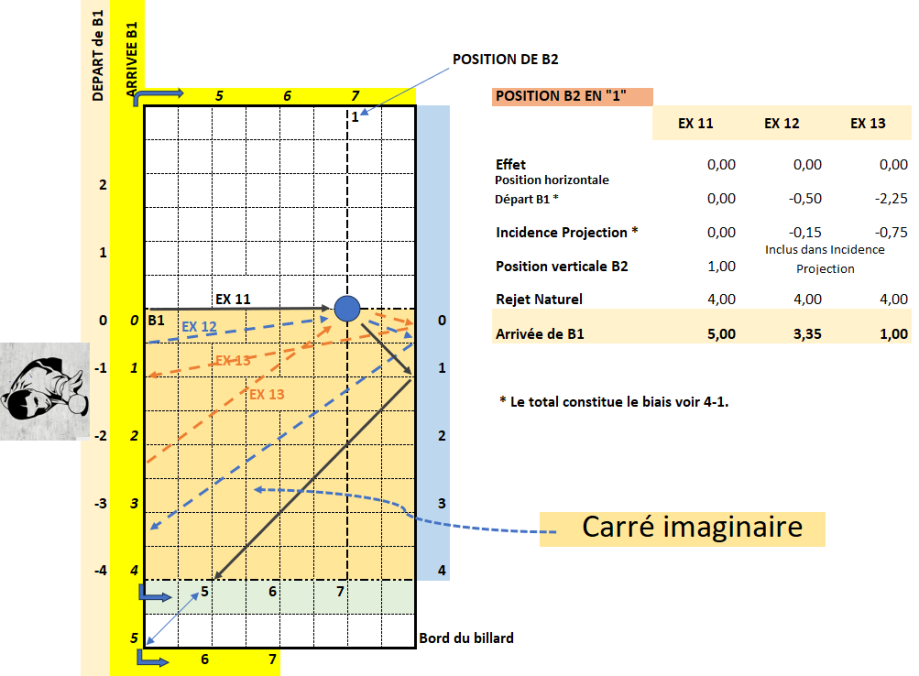
On retrouve les exemples du CAS 4, transposés, mais la logique reste la même.

Évidemment, le calcul s’adapte lorsque que B1 est ‘entre deux mouches’, voir exemples 12 et 13.

Lorsque B1 et B2 sont alignés horizontalement (Cas 11), on tient compte de la position verticale pour calculer l’incidence du rejet à la bande (voir cas 1 et 2 ci-avant).

Lorsque ce n’est pas le cas, il faut tenir compte de l’Incidence Projection (voir cas 4-1).

5-2 POUR UN EXEMPLE SUR UN POINT D’ÉCHELLE EN BORD DU BILLARD.

CAS 5-2

Ce cas permet de visualiser le ‘carré imaginaire’ en bordure de billard, en présentant des cas de points d’échelle.

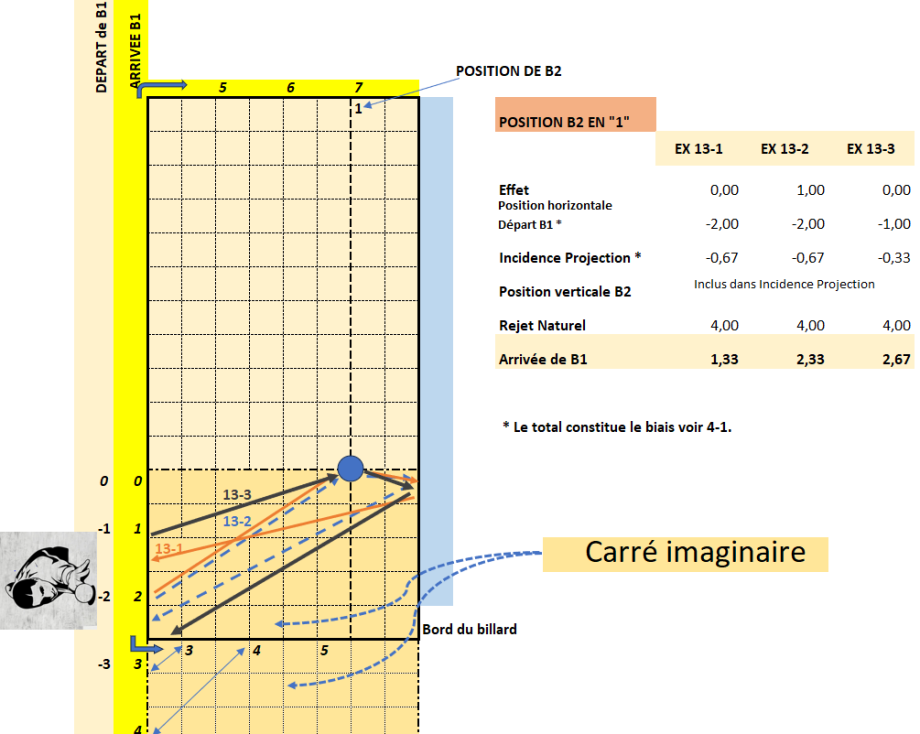
L’incidence est calculée de façon exacte.

On voit ici la figuration de l’arrivée de B1 dans le carré imaginaire ‘en dehors du billard’ (Ex 13-3), ainsi que l’incidence d’un effet de +1 (Ex 13-2 par rapport à 13-1).

5-3 EXEMPLES COMPLÉMENTAIRES ‘EN DEHORS DU BILLARD’.

La démarche est identique à celle du cas 5-2. Il faut compter ‘en dehors du billard’ et suivre la bande en tournant.

5-4 LES POINTS ‘DANS LE VIDE’.

Dans les exemples qui suivent :

On appellera POINTS DANS LE VIDE  les points pour lesquels le départ de B1 a lieu au milieu du billard et se dirige vers une petite bande.

Dans ce cas, il est impossible de s’appuyer sur une bande qui se trouve près de B1 pour décompter le biais.

De même la position de B3 peut être difficile à apprécier.

Voici l’exemple d’une de ces situations :

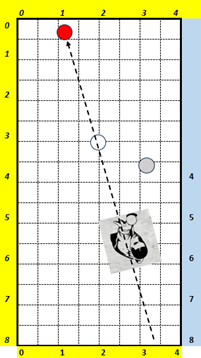
Il s’agit de définir une approche qui permet de déterminer le biais et le trajet de B1.

On utilisera le carré imaginaire comme précédemment.

En fait, par rapport aux cas précédents, le billard se trouve ‘tourné’.

5-4.1  LE CALCUL DU BIAIS.

On va pouvoir utiliser le principe du Carré Imaginaire qui consiste à déplacer mentalement le carré en fonction de la position de B2 qui prend ainsi une position horizontale ‘0’.

Nous allons calculer le biais à partir des positions de B1 et B2.

Dans les exemples suivants, B2 est en position 1 (qui deviendra ‘0’ pour les calculs ultérieurs).

Le calcul de la position de B1 peut s’effectuer ainsi, selon le cas dans lequel on se trouve :

• L’alignement de B1-B2 peut s’apprécier en utilisant les mouches de la petite bande opposée (Cas 1).

• L’alignement de B1-B2 peut s’apprécier en utilisant le principe du Carré Imaginaire (Cas 2).

• L’alignement de B1-B2 ne peut pas s’apprécier selon les deux cas précédents, c’est-à-dire lorsque la projection de l’axe B1-B2 sur la grande bande se situe entre les mouches 4 et 8 (Cas 3).

CAS 1 – BIAIS SUR LA LONGUEUR                                                  CAS 3 – BIAIS AUTRES CAS

                DU BILLARD  

                                                      CAS 2 – BIAIS SUR LE CARRÉ 

                                                                IMAGINAIRE

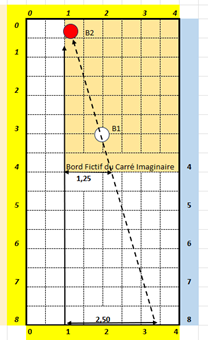
5-4-1-1 CAS 1 : Calcul du biais sur la longueur du billard :

On voit dans notre exemple que le biais sur la longueur du billard est de 2,5 (3,5 en arrivée et 1 en départ).

Le biais sur le demi-billard est donc de 2,5/2 soit 1,25, comme on le voit si l’on observe le franchissement du biais à la position du demi-billard, sur le bord fictif du Carré Imaginaire.

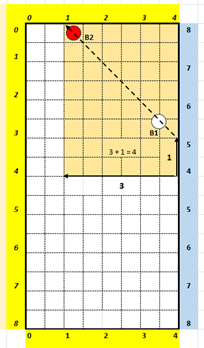
5-4-1-2 CAS 2 : Calcul du biais avec le Carré Imaginaire :

Dans ce cas, on utilise le Carré Imaginaire de la façon habituelle en décomptant sur la petite bande utilisable, puis en repartant du coin du carré à la position 4.

Dans notre exemple, on voit qu’il y a 3 mouches sur la petite bande (on compte sur la petite bande utilisable, puisqu’on ne peut pas compter sur le bord ‘fictif’ du carré imaginaire qui se trouve au milieu du billard), et 1 mouche en repartant du coin du Carré Imaginaire en position 4 sur la grande bande de droite.

Le biais est donc de 3 + 1 = 4 ; ce que l’on confirme visuellement puisque les deux côtés autres que l’hypoténuse ont une longueur égale à 3 mouches.

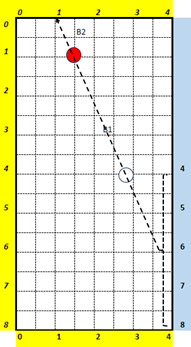
5-4-1-3 CAS 3 : Calcul du biais dans les autres cas :

Cette situation est un peu plus compliquée.

La première étape consiste à calculer le biais à partir de la mouche 4, puis à utiliser un coefficient en fonction de la position à laquelle l’axe B1-B2 coupe la grande bande.

Prenons l’exemple suivant :  

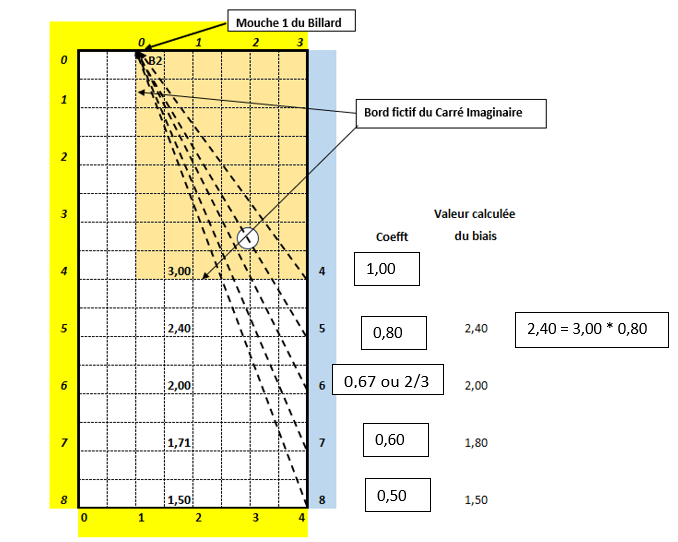
En fonction de la position de B2, on voit que l’axe du biais coupe la petite bande en mouche 1.

La première opération consiste à calculer le biais comme si la droite B1-B2 coupait la grande bande en mouche 4 de la grande bande. Dans l’exemple donné, le calcul donne un résultat de 3, puisque l’axe part de la mouche 1 de la petite bande et va couper la grande bande en position 4.

La difficulté réside dans l’impossibilité de ‘lire’ à quel endroit l’axe B1-B2 franchit le bord fictif du Carré Imaginaire.

On va donc le calculer  à partir du biais de la position à 4 mouches – qu’on appellera Biais-référence - et de l’application d’un coefficient :

• Si B1-B2 coupe la grande bande en mouche 5, le biais est calculé à : 3 * 0,80 = 2,40 ; valeur égale à la valeur réelle qui est de 2,40, ainsi que c’est précisé sur le schéma ci-dessus.

• Si B1-B2 coupe la grande bande en mouche 6, le biais est approximé à : 3 * 0,67 (ou 2/3) = 2,00 ; valeur égale à la valeur réelle qui est de 2,00, ainsi que c’est précisé sur le schéma ci-dessus.

• Si B1-B2 coupe la grande bande en mouche 7, le biais est approximé à : 3 * 0,60 = 1,80 ; valeur proche de la valeur réelle qui est de 1,71[1], ainsi que c’est précisé sur le schéma ci-dessus. Ceci est dû à l’utilisation d’un coefficient arrondi à 0,60 plutôt que le coefficient réel de 4/7 soit 0,5714.

• Si B1-B2 coupe la grande bande en mouche 8, le biais est égal à : 3 * 0,50 = 1,50 ; valeur égale à la valeur réelle, puisque ce cas nous renvoie au cas N°1 de calcul du biais sur la longueur du billard (voir 5-4-1-1 ci-dessus).

[1] Valeur validée par mesure sur papier millimétré.

Prenons un autre exemple :

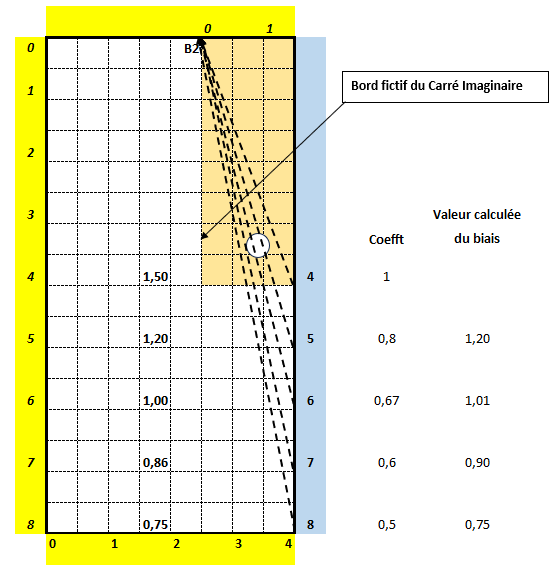
A partir d’un biais-référence de 1,50 pour la mouche 4, on calcule les biais de :   

• 1,20 si l’axe B1-B2 coupe la grande bande en mouche 5, contre un biais réel de 1,20 ;

• 1,01 si B1-B2 coupe la grande bande en mouche 6, contre un biais réel de 1,00 ;

• 0,90 si B1-B2 coupe la grande bande en mouche 7, contre un biais réel de 0,86 ;

• 0,75 si B1-B2 coupe la grande bande en mouche 8, un biais réel de 0,75 (voir 5-4-1-1).

Voici une récapitulation des biais calculés de mouche en mouche, à partir d’un biais de référence mouche 4 – dans la pratique, le résultat des calculs sera arrondi :

Calculs sans arrondi.

5-4.2   PRISE EN COMPTE DU REJET.

5-4.2.1 APPRÉCIATION DU REJET APRÈS CALCUL DU BIAIS DANS LA LONGUEUR.

Le cas se présente ainsi :

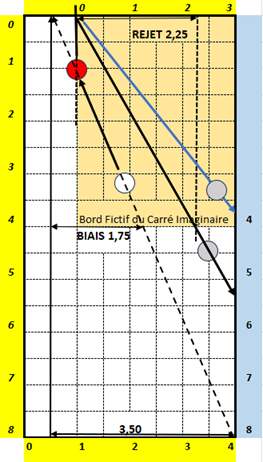
Le biais est de 3,50 dans la longueur, donc de 1,75 apprécié sur le demi-billard (pour le calcul du biais voir 5-4-1-1).

Le rejet est donc de 2,25, soit 4 – 1,75, à partir de la projection horizontale de B2 à la bande.

Le trait plein noir montre le trajet de B1 si le coup est joué sans effet, permettant de caramboler B3 se trouvant sur ce trajet.

Le trait plein bleu montre le trajet de B1 si le coup est joué avec 1 dose d’effet, permettant de caramboler B3 se trouvant sur ce trajet.

Remarque : le rejet est de 2,25 apprécié à la mouche 4 => apprécié à la mouche 5 il est de 2,25/0,80 = 2,81.

On voit que le rejet atteint 3 un peu après la mouche 5.

5-4.2.2 APPRÉCIATION DU REJET EN UTILISANT LE CARRÉ IMAGINAIRE.

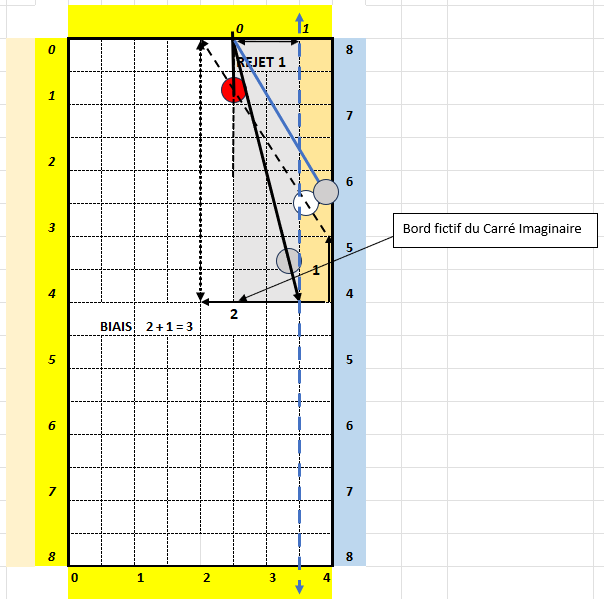
Le biais est de 3 (2 + 1) (pour le calcul du biais voir 5-4-1-2).

Le rejet est donc de 1 (4 – 3) à partir de la projection horizontale de B2 à la bande. Son appréciation est figurée en gris clair. On peut utiliser la projection sur la petite bande en bas (pointillé vertical bleu) pour visualiser le rejet sur le bord fictif du Carré Imaginaire

Comme dans l’exemple précédent, le trait plein noir montre le trajet de B1 si le coup est joué sans effet, permettant de caramboler B3 se trouvant sur ce trajet.

Le trait plein bleu montre le trajet de B1 si le coup est joué avec 1 dose d’effet, permettant de caramboler B3 se trouvant sur ce trajet.

5-4.2.3 APPRÉCIATION DU REJET APRÈS CALCUL DU BIAIS SUR LES MOUCHES  4 À 8.

Rappelons qu’il convient tout d’abord de :

• Déterminer le biais-référence de la mouche 4 ;

• Calculer le biais réel en fonction de l’axe B1-B2 et de son intersection avec la mouche de la grande bande.

• Puis calculer ensuite le rejet qui sera égal à 4 moins le biais réel.

Prenons l’exemple suivant :

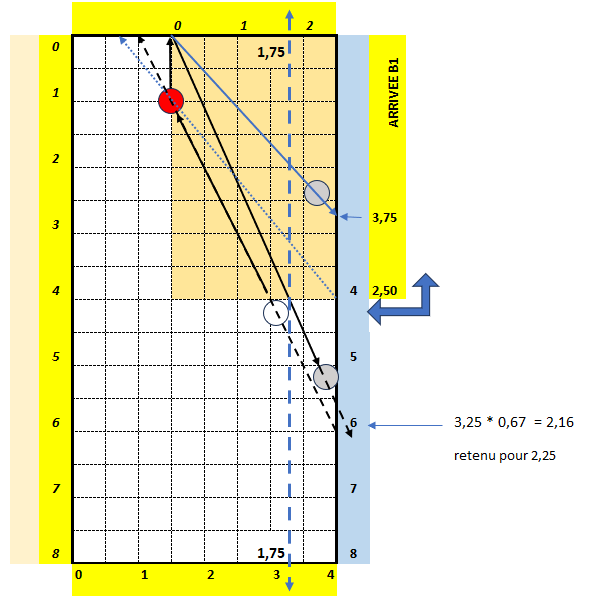
Le biais-référence (tracé petit pointillé bleu) est de 3,25.

On voit que l’axe B1-B2 coupe la grande bande en mouche 6, donc le biais réel est de 3,25 * 0,67 soit 2,16.

(calcul mental : 3 * 0,67 ou 2/3 = 2,00  +  (0,25 * 0,67 ou 2/3) = 0,16 car 25/3 = 8 donc 2/3 è 16, d’où 2,16)

On retient un résultat de 2,25 plus simple à utiliser (au lieu de 2,16).

Le rejet est donc de 4 – 2,25 = 1,75, apprécié au niveau de la mouche 4.

On peut le visualiser en prenant l’axe entre les 2 petites bandes matérialisé par l’axe vertical gros pointillé bleu.

Le trait plein noir montre le trajet de B1 si le coup est joué sans effet, permettant de caramboler B3 se trouvant sur ce trajet, coupant le bord fictif du Carré Imaginaire en 1,75.

Le trait plein bleu montre le trajet de B1 si le coup est joué avec 2 doses d’effet, permettant de caramboler B3 se trouvant sur ce trajet, et coupant le Carré Imaginaire en 3,75 (compter en tournant, sachant que l’angle du Carré Imaginaire correspond à 2,50).

Remarque : le rejet est de 1,75 apprécié à la mouche 4 => apprécié à la mouche 5, il est de 1,75/0,80 = 2,19. Ce que l’on constate sur le schéma. (noter que 1,75/0,80 = 1,75*1,25 soit 1,75 + 1,75/4 ; sachant que 1,75/4 peut être retenu pour 0,40 (0,40*4 = 1,60) et donc on aurait : 1,75 + 0,40 = 2,15, chiffre peu différent de 2,19).

Apprécié à la mouche 6, il est de 1,75/0,67 = 2,61 ; on voit que le trajet de B1 coupe la grande bande, c’est-à-dire le repère 2,50, un peu avant la mouche 6. (noter que 1,75/0,67 = 1,75 * 1,50 = 1,75 + 1,75/2, soit 1,75 + 0,88 = 2,63).